People are often mixing the above as if they were one and the same, so here’s a recap of them. One of the things you often find people saying is that “my data is in the WGS84 coordinate system”. This doesn’t really make sense, but I will get back to this later.
This is a very confusing subject, and I might have gotten a few things wrong myself, so please add a comment and I’ll update it ASAP.
Coordinate systems
A coordinate system is simply put a way of describing a spatial property relative to a center. There is more than one way of doing this:
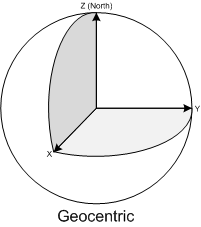
- The Geocentric coordinate system is based on a normal (X,Y,Z) coordinate system with the origin at the center of Earth. This is the system that GPS uses internally for doing it calculations, but since this is very unpractical to work with as a human being ( due to the lack of well-known concepts of east, north, up, down) it is rarely displayed to the user but converted to another coordinate system.
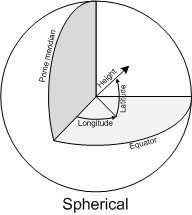
- The Spherical or Geographic coordinate system is probably the most well-known. It is based on angles relative to a prime meridian and Equator usually as Longitude and Latitude. Heights are usually given relative to either the mean sea level or the datum (I’ll get back to the datum later).
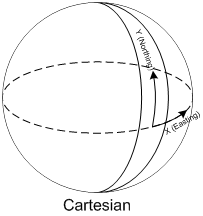
- The Cartesian coordinate system is defined as a “flat” coordinate system placed on the surface of Earth. In some projections it’s not flat in the sense that it follows the earth’s curvature in one direction and has a known scale-error in the other direction relative to the distance of the origin. The most well-known coordinate system is the Universal Transverse Mercator (UTM), but surveyors define their own little local flat coordinate systems all the time. It is very easy to work with, fairly accurate over small distances making measurements such as length, angle and area very straightforward. Cartesian coordinate systems are strongly connected to projections that I will cover later.
Sidenote: The geocentric coordinate system is strictly speaking a cartesian coordinate system too, but this is the general terms I've seen used the most when talking about world coordinate systems.
Datums and ellipsoids
Some of the common properties of the above coordinate systems are that they are all relative to the center of Earth and except the Geocentric coordinate system, uses a height system relative to the surface of the earth.
This poses two immediate problems:
- Where is the center of the earth
- What is the shape of the earth?
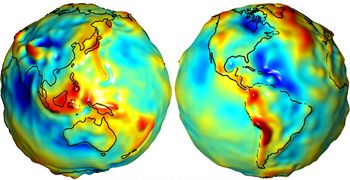 By now most people should know that that the earth isn’t flat (although there are still some who doubts it). If we define the surface of Earth as being at the mean sea level (often referred to as the Geoid), we don’t get a spheroid or even an ellipsoid. Because of gravitational changes often caused by large masses such as mountain ranges etc, Earth is actually very irregular with variations of +/- 100 meters. Since this is not very practical to work with as a model of earth, we usually use an ellipsoid for approximation. The ellipsoid is defined by its semi-major axis, and either the flattening of the ellipoid or the semi-minor axis.
By now most people should know that that the earth isn’t flat (although there are still some who doubts it). If we define the surface of Earth as being at the mean sea level (often referred to as the Geoid), we don’t get a spheroid or even an ellipsoid. Because of gravitational changes often caused by large masses such as mountain ranges etc, Earth is actually very irregular with variations of +/- 100 meters. Since this is not very practical to work with as a model of earth, we usually use an ellipsoid for approximation. The ellipsoid is defined by its semi-major axis, and either the flattening of the ellipoid or the semi-minor axis.
The center and orientation of the ellipsoid is what we call the datum. So the datum defines an ellipsoid and through the use of a set of points on the ground that we relate to points on the ellipsoid, we define the center of the Earth. This poses another problem, because continental drift moves the points used to define the points around all the time. This is why the name of a datum usually have a year in it, often referring to the position of those points January 1st of that year (although that may vary).
There are a vast amount of datums, some used for measurements all over the world, and other local datums defined so they fit very well with a local area. Some common ones are: World Geodetic Datum 1984 (WGS84), European Datum 1950 (ED50) and North American Datum 1983 (NAD83).
The most well-known is WGS84 used by the GPS systems today. It is a good approximation of the entire world and with fix-points defined almost all over the world. When it was defined they forgot to include points in Europe though, so the Europeans now have their own ETRS89, which is usually referred to as the “realization of WGS84 in Europe”. The problem here was solely because of continental drift, so they defined some points relative to WGS84 in 1989, and keeps track of the changes. In most use-cases it is of no real importance and you can use one or the other.
I mentioned earlier that people often refer to having their data in WGS84, and you see now why this doesn’t make sense. All you know from that is that the data is defined using the WGS84 datum, but you don’t know which coordinate system it uses.
Read more on Datums and Spheroids.
Projections
The earth isn’t flat, and there is no simple way of putting it down on a flat paper map (or these days onto a computer screen), so people have come up with all sorts of ingenious solutions each with their pros and cons. Some preserves area, so all objects have a relative size to each other, others preserve angles (conformal) like the Mercator projection, some try to find a good intermediate mix with only little distortion on several parameters etc. Common to them all is that they transform the world onto a flat Cartesian coordinate system, and which one to choose depends on what you are trying to show.
A common statement that I hear in GIS is the following “My map doesn’t have a projection”, but this is simply not possible (unless you have a good old rotating globe). Often people are referring to data that is in longitude/latitude and displayed on a map without having specified any projection. What happens is that the system applies the simplest projection it can: Mapping Longitude directly to X and Latitude to Y. This results in an equirectangular projection, also called the “Plate Carree” projection. It results in very heavy distortion making areas look squashed close to the poles. You can almost say that the “opposite” of the Plate Carree is the Mercator projection which stretches areas close to the poles in the opposite direction, making them look very big. Mercator is the type of projection you see used on Live maps and Google maps, but as many often mistakenly thinks, they do NOT use WGS84 for the projected map, although WGS84 is used when you directly input longitude/latitude values using their API (read more on this here).
More on projected coordinate systems
Spatial reference
The spatial reference is a combination of all the above. It defines an ellipsoid, a datum using that ellipsoid, and either a geocentric, geographic or projection coordinate system. The projection also always has a geographic coordinate system associated with it. The European Petroleum Survey Group (EPSG) has a huge set of predefined spatial references, each given a unique ID. These ID’s are used throughout the industry and you can download an Access database with all them from their website, as well as some very good documents on projection (or see the Spatial References website).
So when you hear someone saying they have their data in WGS84, you can often assume that they have longitude/latitude data in WGS84 projected using Plate Carree. The spatial reference ID of this is EPSG:4326.
Spatial References are often defined in a Well-known format defining all these parameters. The Spatial Reference EPSG:4326 can therefore also be written as:
GEOGCS["GCS_WGS_1984",DATUM["D_WGS_1984",SPHEROID["WGS_1984",6378137,298.257223563]],PRIMEM["Greenwich",0],UNIT["Degree",0.0174532925199433]]
As mentioned Live/Google maps use a Mercator projection, but although their datum is based on WGS84, they use a sphere instead of an ellipsoid. This means that they use the same center and orientation as WGS84, but without applying any flattening. The spatial reference string for their projection therefore becomes:
PROJCS["Mercator Spheric", GEOGCS["WGS84based_GCS", DATUM["WGS84based_Datum", SPHEROID["WGS84based_Sphere", 6378137, 0], TOWGS84[0, 0, 0, 0, 0, 0, 0]], PRIMEM["Greenwich", 0, AUTHORITY["EPSG", "8901"]], UNIT["degree", 0.0174532925199433, AUTHORITY["EPSG", "9102"]], AXIS["E", EAST], AXIS["N", NORTH]], PROJECTION["Mercator"], PARAMETER["False_Easting", 0], PARAMETER["False_Northing", 0], PARAMETER["Central_Meridian", 0], PARAMETER["Latitude_of_origin", 0], UNIT["metre", 1, AUTHORITY["EPSG", "9001"]], AXIS["East", EAST], AXIS["North", NORTH]]